كان مكعب روبيك أحد الألغاز المفضلة في العالم لمدة 40 عاماً مضت. اُبتكرت طرقٌ عدة مختلفة لحلها، كما هوّ موضح في عددٍ لا يحصى من الكتب التي تناولتها. لكن خبراء حل هذه اللعبة -«سبيدكيوبرز»- يستطيعون حلها في بضع ثوان.
وبالإضافة إلى إتقان حل مكعب روبيك، هناك العديد من الحقائق الرياضية المتعلّقة به. هناك إمكانية لتدوير أحد الوجوه الستة للمكعب بمقدار 90 أو 180 أو 270 درجة، وبذلك تبلغ عدد الحركات المُحتملة الكلية 43,252,003,274,489,856,000 حركة لحل لغز مكعب روبيك.
وبالرغم من هذا التعقيد، فقد تبيّن عام 2010 أنه يمكن حل مكعب روبيك في 20 حركة أو أقل دائماً، وذلك بغض النظر عن الحالة الأولية أو درجة التعقيد التي يكون عليها المكعّب عند البدء بحلّه. يشار إلى هذا الرقم باسم «الرقم المُقدّس»، حيث أن جميع طرق الحل المعروفة التي يستخدمها البشر تستخدم عادة حركاتٍ أكثر بكثير من هذه القيمة المثلى.

ولكن ماذا عن السؤال المعاكس؛ كم عدد الحركات المطلوبة لبعثرة (خلط) مكعب روبيك محلول؟ قد يبدو هذا السؤال للوهلة الأولى أسهل بكثير من حساب الرقم المقدّس، لكن عموماً، لا يحتاج خلط مكعب روبيك -على النقيض من حلّه- أي مهاراتٍ على الإطلاق.
لقد تمت الإجابة على أسئلةٍ مشابهة في السابق بالنسبة لعملية خلط أوراق اللعب. من الأمثلة الشهيرةِ على ذلك دراسة «خلط أوراق اللعب» عام 1990 التي أجراها عالما الرياضيات «ديف باير وبيرسي دياكونيس»، حيث يعرفّان مجموعة البطاقات بأنّها «مختلطة» إذا كان ترتيب الأوراق فيها عشوائياً، ويملك كلّ ترتيبٍ ممكن نفس الاحتمالية في الظهور. وقد أظهر باير ودياكونيس أن خلط الأوراق 7 مرّاتٍ ضروري وكافٍ للحصول على خليطٍ عشوائي قياسي من أوراق اللعب.
وفي العام الماضي، نشر علماء الرياضيات دراسةً مماثلة عن حلّ لغز (15)، وهو رقعةٌ مكوّنة من 4*4 مربع فيها 15 لوحةً مرقّمةً من 1 إلى 15، ويمكن تحريكها لكي يتم ترتيبها مع توّفر مساحةِ مربعٍ واحدٍ فارغ.
ماذا يعني خلط مكعب روبيك؟
سيقوم الشخص العادي الذي يحاول خلط مكعّب روبيك المحلول بإجراء حركاتٍ عشوائية غير محددة عليه. يعتبر علماء الرياضيات تسلسل هذه الحركات العشوائي حالةً خاصّة، يطلقون عليها سلسلة ماركوف، والتي تقول خاصيتها الرئيسية إنّ احتمال ما ستكون عليه الحالة التالية لا يعتمد على أيٍّ من الحالات السابقة.
عند تطبيق نظرية سلاسل ماركوف على عملية خلط المكعّب، فإنه مع زيادة عدد الحركات العشوائية، يصبح احتمال حدوث أي حالةٍ بعينها أقرب وأقرب من ناتج قسمة الرقم 1 على 43,252,003,274,489,856,000. يطلق علماء الرياضيات على ذلك «التوزيع المنتظم المستمر»، حيث أن كل حالةٍ ممكنة الحدوث بنفس الاحتمال.
بعد أي عددٍ معين من حركات البعثرة العشوائية، ستكون حالة المكعب عشوائية، ولكن توزيع هذا الاحتمالي لن يكون موحداً تماماً؛ بعض الحالات ستكون أكثر عرضة للتكرار من غيرها.
ليكن التابع [دي «تي»] الذي يوّصف مدى بُعدِ توزّع الاحتمالات عند عددٍ معين من الحركات العشوائية «تي» عن توزّع الاحتمال المنتظم المستمر، إذاً كلما زاد عدد التحركات العشوائية تي، ستنخفض بالتالي قيمة [دي «تي»]. المكعب الذي تتم بعثرته يتوافق مع كون [دي «تي»] صغير القيمة.
سلسلة ماركوف مونتي كارلو
يُسمّى هذا الإنخفاض وفق نظرية سلاسل ماركوف بـ «الخلط» فإلى جانب تطبيقاتها في عملية خلط الأوراق، فإن نظرية خلط سلسلة ماركوف لها أيضاً تطبيقات عملية مهمّة جداً. وتُعدّ نظرية ماركوف مونتي كارلو واحدةً من أهمّ الأدوات الحسابية في العلوم والهندسة الحديثة. وهذه الطريقة التي سميت نسبةٍ إلى كازينو مونتي كارلو، تعتمد بشكل أساسي على الصدفة، وفي جوهرها، تحاول حل المشكلات الرياضية الصعبة تقريبياً باستخدام تخمينات عشوائية متعددة.
في الممارسة العملية، غالبا ما تستخدم سلاسل ماركوف لإنتاج هذه الحالات العشوائية. لفهم دقة أساليب سلسلة مونتي كارلو هذه من سلسلة ماركوف، فإن مهمتها الأساسية تتمثل في تقدير سرعة تناقص [دي «تي»] عند زيادة قيمة (تي).

تعدُ دراسة مشكلة بعثرة مكعّب روبيك ثلاثي الأبعاد 3*3*3 القياسي تحدياً رائعاً لم يُحلّ بعد. ومع ذلك، يصبح سهلاً حله إذا ما ركّزنا انتباهنا إلى الإصدار الثنائي الأصغر منه 2*2*2، والذي يُسمّى مكعّب الجيب.
تغيب الحواف والقطع الوسطى في هذا المكعّب وتبقى قطع الزاوية فقط. ويبلغ عدد الحالات الممكنة في المكعب الجيبي 3.674.160 حالة ممكنة، والرقم المقدّس هو 11 فقط.
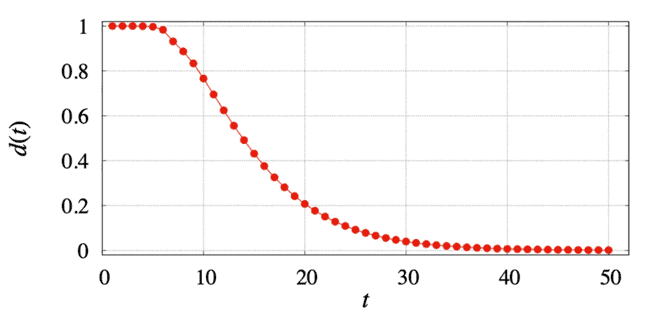
يظهر في الرسم البياني أدناه تمثيلٌ للتابع [دي «تي»] لمكعّب الجيب. حيث يظهر أنه بعد 11 حركة، لا يزال [دي «تي»] كبيراً جداً عند قيمة 0.695. القيمة الأولى لـ «تي» التي تعطي قيمةً لـ [دي «تي»] أقلّ من 0.25 (والتي تُدعى «وقت الخلط» في نظرية سلسلة ماركوف) هي 19. بعد 25 حركة، تبلغ قيمة [دي «تي»]= 0.092، وبعد 50 حركة يصبح 0.0012، بينما يبلغ بعد 100 حركة 0.00000017.
وبالطبع، بمجرد أن تبعثر المكعب، كل ما تبقى عليك هو حلها مرة أخرى.

