في 20 مارس من العام 2018، فاز الرياضي الأميركي الكندي روبرت لانغلاندز بجائزة آبل Abel (جائزة دولية تمنحها سنوياً الجمعية الرياضياتية النرويجية)، تقديراً لإنجازاته في الرياضيات طوال حياته. حيث أظهرت أبحاث لانغلاندز كيف يمكن الجمع بين مفاهيم من الهندسة، والجبر، والتحليل عن طريق عامل مشترك يربطها بالأعداد الأولية.
عندما يقوم ملك النرويج بتقديم الجائزة للانغلاندز في مايو، فإنه سيكرّم بذلك أحدث الجهود الساعية إلى فهم الأعداد الأولية على مدى 2,300 عام، والتي يمكن القول إنها تمثل أكبر وأقدم مجموعة من البيانات في تاريخ الرياضيات.
باعتباري عالماً في الرياضيات كرس وقته لدراسة "برنامج لانغلاندز"، فإنني مبهور بتاريخ الأعداد الأولية وكيف تمكنت التطورات الأخيرة من سبر أسرارها. لماذا أسرت الأعداد الأولية علماء الرياضيات لآلاف السنين؟
كيف تعثر على الأعداد الأولية
لدراسة الأعداد الأولية، يقوم الرياضيون بتمرير كافة الأعداد عبر مراحل تصفية متتالية إلى أن يبقى منها الأعداد الأولية فقط. قامت عملية الغربلة هذه بإنتاج جداول من ملايين الأعداد الأولية خلال القرن التاسع عشر. هذه العملية تسمح لحواسيب اليوم بالعثور على مليارات الأعداد الأولية في أقل من ثانية. ولكن الفكرة الأساسية لعملية الغربلة هذه لم تتغير على مدى 2,000 عام.
كتب عالم الرياضيات إقليدس في العام 300 قبل الميلاد يقول: "العدد الأولي هو العدد الذي يقاس بالوحدة فقط". هذا يعني أن الأعداد الأولية لا يمكن تقسيمها بالتساوي على أي عدد أصغر منها باستثناء العدد 1. وقد اتفق الرياضيون على عدم اعتبار العدد 1 كعدد أولي.
برهن إقليدس أن الأعداد الأولية مجموعة غير منتهية – فهي تتوالى بلا نهاية – ولكن المعلومات التاريخية تشير إلى أن إراتوستينس هو من قدم لنا طريقة الغربلة التي تساعد في سرد الأعداد الأولية بسرعة.
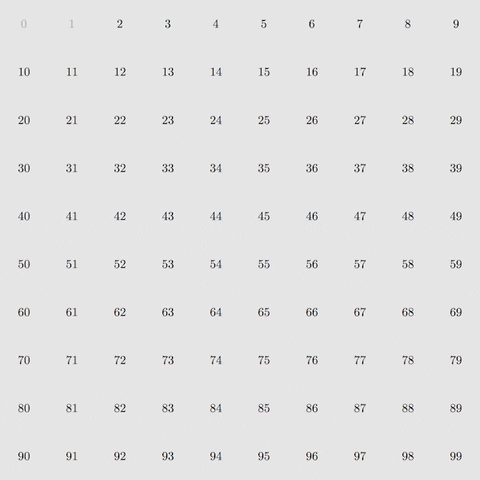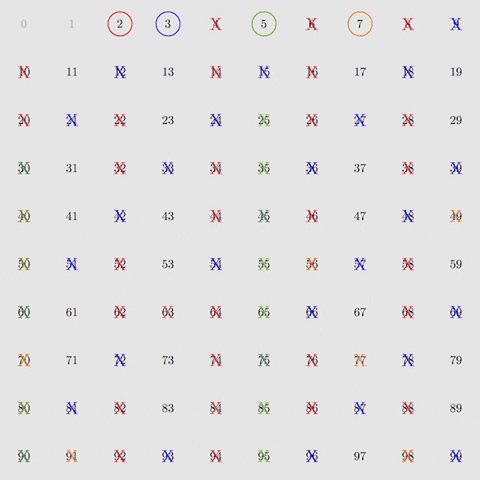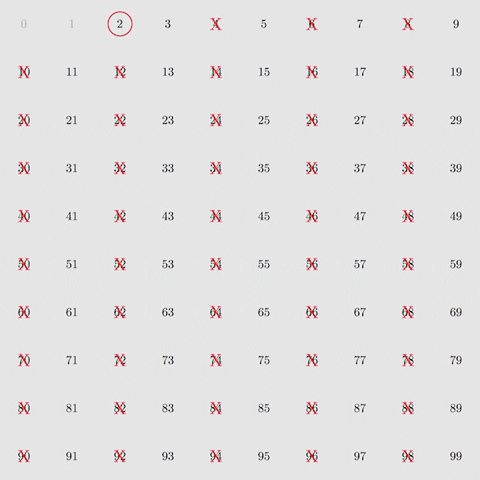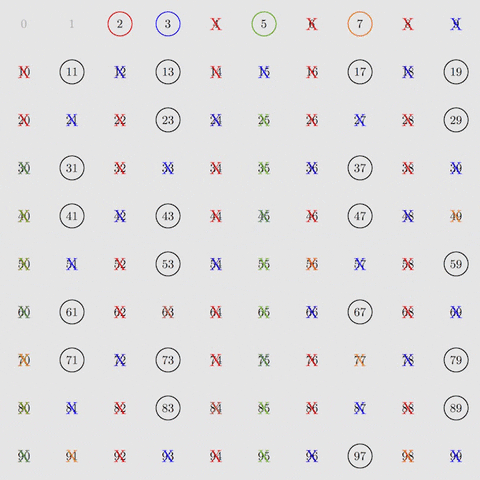
إليكم فكرة الغربلة (الاستبعاد). أولاً، نقوم باستبعاد مضاعفات الأعداد 2، ثم 3، ثم 5 ثم 7، وهي الأعداد الأولية الأربعة الأولى. وإذا طبقنا ذلك مع جميع الأعداد من 2 إلى 100، فسيتبقى لدينا الأعداد الأولية فقط.
بواسطة GIPHY
باتباع 8 خطوات من الفلترة، يمكننا أن نعزل الأعداد الأولية حتى الرقم 400. وباتباع 168 خطوة من الفلترة، يمكننا أن نعزل الأعداد الأولية حتى 1 مليون. هذه يوضح لنا قوة عملية الغربلة التي قدمها إراتوستينس.
الكثير من الجداول
يعد جون بيل من أوائل الأسماء التي اشتهرت في جدولة الأعداد الأولية، وهو عالم رياضيات إنجليزي كرس نفسه لإنشاء جداول من الأرقام المفيدة.
كان متحمساً لحل المسائل الحسابية القديمة التي طرحها العالم اليوناني ديوفانتوس، ولكن سعيه الشخصي أيضاً دفعه نحو تنظيم الحقائق الرياضية. بفضل الجهود التي بذلها، تم نشر الأعداد الأولية حتى الرقم 100,000 على نطاق واسع في أوائل القرن الثامن عشر.
وبحلول العام 1800، عمل عدد من المشاريع المستقلة على جدولة الأعداد الأولية حتى الرقم 1 مليون.
لكي تتم أتمتة خطوات الغربلة المملة، قام عالم رياضيات ألماني يدعى كارل فريدريش هيندينبرج باستخدام شرائط تمرير قابلة للتعديل لاستبعاد المضاعفات على امتداد صفحة كاملة من جدول الأعداد في آن واحد.
وهناك أسلوب آخر ذو تقنية بسيطة اعتمد على استخدام المرسام (الاستنسل) لتحديد مواقع المضاعفات في الجداول. حيث بدأ عالم الرياضيات جاكوب كوليك بحلول منتصف القرن التاسع عشر بالعمل على مشروع طموح للعثور على جميع الأعداد الأولية حتى الرقم 100 مليون.

حقوق الصورة: أواو، ناكلاس كوليك، الصورة مقدمة من دينيس روجيل، مقدمة من المؤلف
ربما كانت هذه "البيانات الكبيرة" التي تعود إلى القرن التاسع عشر قد لعبت دور جدول مرجعي فحسب، وذلك في حال لم يكن كارل فريدريش غاوس قد قرر تحليل الأعداد الأولية في حد ذاتها. بعد أن حاز غاوس على قائمة من الأعداد الأولية وصلت إلى الرقم 3 ملايين، بدأ بعدّها ألفاً تلو أخرى (في كل مرة يعدّ مجموعة من 1000 عدد أولي).
حيث قام بعدّ الأعداد الأولية حتى الرقم 1,000، ثم الأعداد الأولية التي تقع بين 1,000 والرقم 2,000، ثم الأعداد الأولية التي تقع بين 2,000 والرقم 3,000، وهكذا دواليك.
اكتشف غاوس أنه كلما وصل في العد إلى أرقام أعلى، يقل تواتر الأعداد الأولية بشكل تدريجي وفقاً لقانون "اللوغاريتم المقلوب". فقانون غاوس لا يظهر كم يوجد من الأعداد الأولية بالضبط، ولكنه يوفر تقديراً جيداً للغاية. على سبيل المثال، يتنبأ قانونه بوجود 72 عدد أولي بين الرقمين 1,000,000 و 1,001,000، والعدد الصحيح هو 75 عدد أولي، أي بتقدير خاطئ يقارب 4%.
بعد مرور قرن على الاكتشافات الأولى لغاوس، تم إثبات قانونه في مبرهنة الأعداد الأولية. حيث تقترب نسبة الخطأ المئوية من الصفر كلما أصبح المجال الرقمي للأعداد الأولية أكبر فأكبر. كما أن فرضية ريمان، وهي مسألة مطروحة للحل اليوم مقابل جائزة بمليون دولار، توضح مدى الدقة الفعلية لتقدير غاوس.
إن كلاً من مبرهنة الأعداد الأولية وفرضية ريمان تحظى بالاهتمام والمال معاً، ولكن كلتيهما تتبعان عمليات تحليل سابقة للبيانات أقل جاذبية.
ألغاز الأعداد الأولية الحديثة
اليوم، أصبحنا نحصل على مجموعات البيانات من البرامج الحاسوبية بدلاً من الاستنسل اليدوي، ولكن علماء الرياضيات لا يزالون يبحثون عن أنماط جديدة بين الأعداد الأولية.
باستثناء العددين 2 و5، فإن جميع الأعداد الأولية تنتهي بأحد الأرقام 1، 3، 7، أو 9. في القرن التاسع عشر، ثبُتَ أن هذه الأرقام الأخيرة المحتملة تتكرر بشكل متساوٍ. بعبارة أخرى، إذا نظرنا إلى الأعداد الأولية حتى الرقم 1 مليون، فإن حوالي 25% منها تنتهي بالرقم 1، و25% منها تنتهي بالرقم 3، و25% تنتهي بالرقم 7، و25% تنتهي بالرقم 9.
الأرقام الأخيرة التي تظهر في الأعداد الأولية
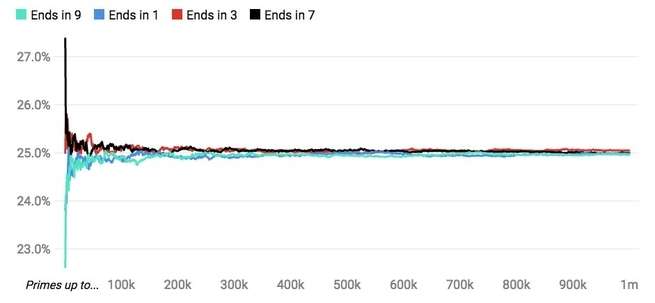
مصدر الصورة: مارتن ويسمان
قبل بضع سنوات، تفاجأ باحثا الأعداد في جامعة ستانفورد؛ ليمكي أوليفر و كانان سوانداراراجان بوجود ميزات غريبة تتعلق بالأرقام الأخيرة للأعداد الأولية. حيث قاما بتجربة تنظر إلى الرقم الأخير من عدد أولي معين، وتنظر في الوقت نفسه إلى الرقم الأخير من العدد الأولي الذي يليه مباشرة. على سبيل المثال، فإن العدد الأولي الذي يلي العدد الأولي 23 هو العدد 29: حيث يظهر الرقمان 3 و9 في آحادهما. فهل يمكننا أن نرى الثنائية المتتالية (3، 9) أكثر مما نرى الثنائية المتتالية (3، 7) ضمن الأرقام الأخيرة (الخانات الأخيرة) من الأعداد الأولية؟
فقد توقع باحثا الأعداد وجود بعض الاختلافات، ولكن ما وجداه تجاوز التوقعات بكثير. فقد ظهرت فجوات مختلفة تفصل بين الأعداد الأولية؛ على سبيل المثال، يبتعد العدد 23 عن العدد 29 بمقدار 6. ولكن أزواج الأعداد الأولية المتتالية التي ينتهي أولاها بالرقم 3 وثانيها بالرقم 9 (مثل العددين 23 و 29) هي أكثر شيوعاً بكثير من أزواج الأعداد الأولية المتتالية التي ينتهي أولاها بالرقم 7 وثانيها بالرقم 3، على الرغم من أن كلا النوعين من الأزواج لديهما نفس المسافة البينية الفاصلة وهي 6.

حقوق الصورة: م. هـ. ويسمان، وفق رخصة المشاع الإبداعي الكاملة CC-BY
سرعان ما وجد علماء الرياضيات تفسيراً معقولاً لهذا الظاهرة. ولكن، عندما يتعلق الأمر بدراسة الأعداد الأولية المتتالية، فإن عمل الرياضيين يقتصر (غالباً) على تحليل البيانات واللجوء إلى الإقناع. يبدو أن البراهين، والتي تعد المعيار الذهبي عند الرياضيين لتفسير صحة الأشياء، لا زالت تفصلنا عنها عقودٌ من الزمن.