ما التفسير الرياضي لمليارات مليارات الاحتمالات لتكوين مربع روبيك؟

توجد 8 زوايا للمكعب ثلاثية الألوان و12 قطعة تقع بين الزوايا ثنائية الألوان و6 تقع في منتصف كل وجه وهذه ثابتة لا تتحرك.

الحسابات الرياضية للاحتمالات في مكعب روبيك

إن حساب مواقع القطع الثماني في الزوايا المختلفة هو مضروب 8، ويمكن اختيار أحد الثلاثة ألوان لكل قطعة ليظهر للناظر، بالتالي تباديل المواقع تكون مضروب 8 ==> 8*7*6*5*4*3*2*1 = 40320 ووضع كل قطعة في المكان الواحد بثلاث طرق (المقصود تغيير الاتجاه للون) فيكون 3*3*3*3*3*3*3*3 = 6561 وهنا لم نستخدم مضروب الثلاثة لموقع الألوان لأن أماكنها ثابتة لذلك استخدمنا الرقم 3 بدون مضروب.

احتساب مواقع القطع ثنائية الألوان وعددها 12 قطعة، حيث يمكن أن توضع في 12 مكاناً مختلفاً، ولذلك عدد الاحتمالات 12*11*10*9*8*7*6*5*4*3*2*1 = 479001600 ويمكن وضع القطعة الواحدة في المكان الواحد بطريقتين (المقصود قلب القطعة في المكان الواحد) 2*2*2*2*2*2*2*2*2*2*2*2 = 4096

يكون مجموع الاحتمالات المختلفة هو حاصل ضرب الأرقام الأربعة

3^8 * 8! * 2^12 * 12!

6561 * 40320 * 4096 * 479001600 = 519,024,039,293,878,272000 على الآلة الحاسبة وفي الإكسل 519024039293878000000

لكن القطع المختلفة لا تتحرك منفردة، فعند تحريك زاوية تتحرك معها 3 زوايا أخرى و4 قطع وسطية بنفس الحركة، وهذا يقلل الاحتمالات بعدد 3 مضروب بالرقم 4، وينطبق ذلك أيضا عند الرغبة بتحريك قطع وسطية حيث تتحرك معها 4 زوايا و3 قطع وسطية أخرى، لذلك يقسم الرقم السابق على 12

519024039293878000000÷ 12 = 43252003274489900000 في الإكسل وعلى الآلة الحاسبة 43252003274489856000

هناك طريقة أخرى قرأت عنها قبل سنوات بحيث تستخدم الصورة التالية:

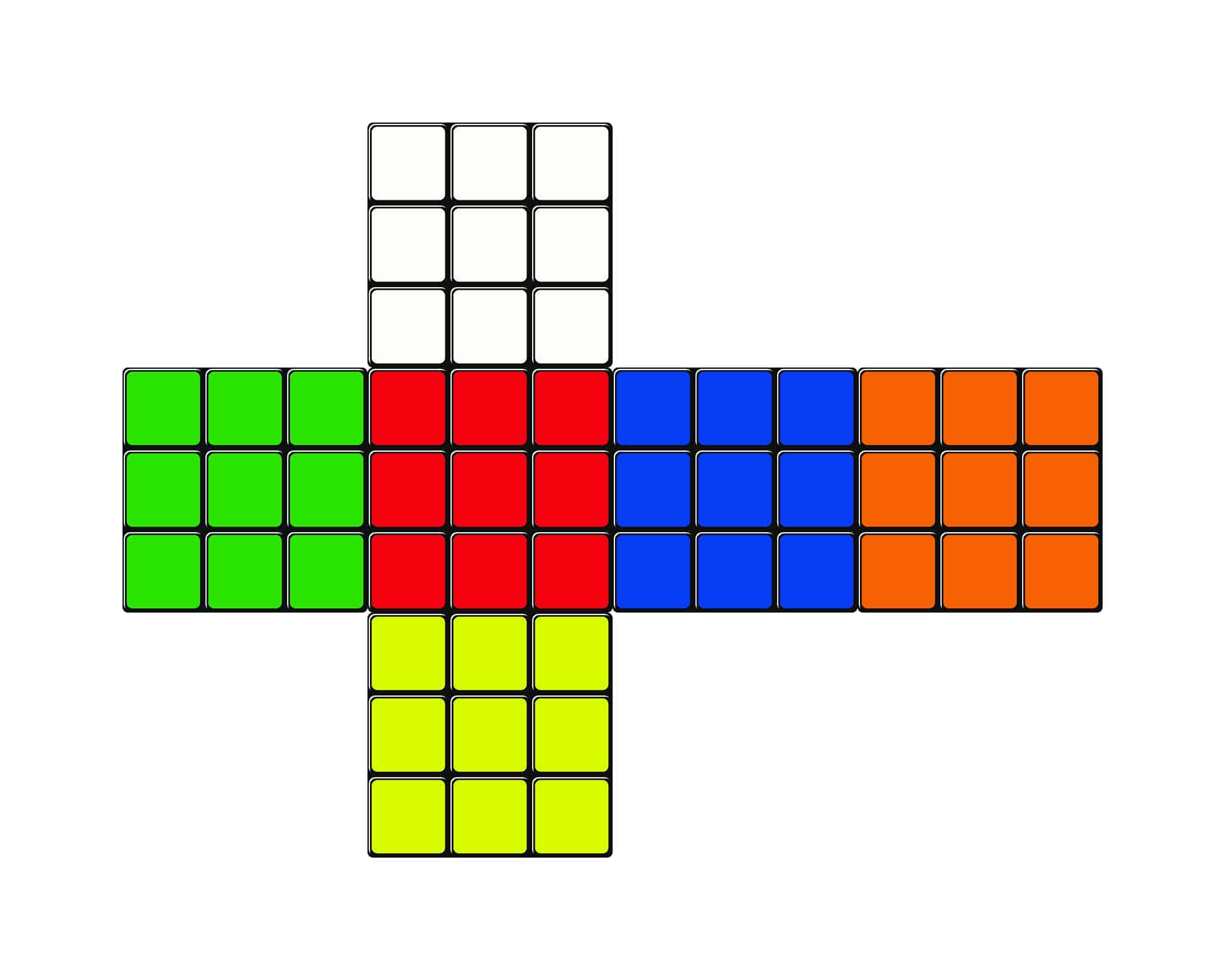
ما التفسير الرياضي لمليارات مليارات الاحتمالات لتكوين مربع روبيك؟ — حقوق الصورة: shutterstock.com/ sonia.eps

حيث يوجد 9 * 6 مكان لوضع الألوان المختلفة بعدد خانات 54 خانة، فيكون الناتج مضروب الرقم 54

54!، وحسب الإكسل 230843697339241* 10^57

لكن كل لون مكرر بعدد 9 مواقع، لذلك تتم القسمة على مضروب 9 وللألوان الستة

54! ÷ (9! * 9! * 9! * 9! * 9! * 9!) = 366862108037088* 10^29

اقرأ أيضاً: ما مدى صعوبة «خلط» مكعب روبيك؟

نشرت هذه المقالة ضمن اتفاقية الشراكة التحريرية بين مجرة وكورا. وتمت الإجابة عن السؤال على موقع كورا بواسطة زياد جمهاوي، حاصل على دكتوراة في الذكاء الاصطناعي وخوارزميات البحث.